

In general a few examples on how to evaluate piecewise functions with different values of x (ex. This video gives a great overview of basic piecewise functions and graphing. Here are a couple great videos explaining and demonstrating piecewise functions. So, each ticket sold would have its own function defining it, specifically in the form of y=Px, x=x When you are selling tickets to the opera, the rate of change for the graph between whole integers is 0 (each section of the graph between integers is flat).
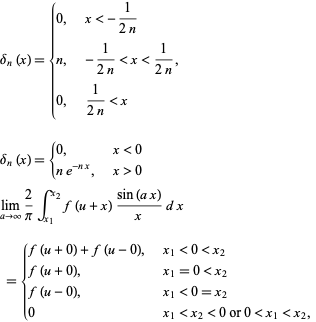
Because you can't sell portions of a ticket the graph technically cannot be linear, it must have interruptions after each integer. Tickets cannot be sold in parts, as only one person will occupy one seat at a time It would be impractical to sell 1.5 tickets, for example. If someone wanted to create a strict representation of total revenues earned against number of tickets sold, they would have to use a piecewise graph. Take, for example, when you sell tickets to the opera. Piecewise functions are useful because they can show a situation where the graph changes radically and to a point outside of the equations range, as often happens in real life. The reason behind their correlation with piecewise functions are they share the same idea of small line segments. They are also called linear piecewise function graphs. Step Functions: are functions that look like steps when plotted on a graph and they follow the same piecewise rules. In order for a function to be differentiable it must satisfy two conditions:Ģ) The "pieces" must match with the same slope In graphing this function we realize it is not differentiable, because when you take the derivative the two pieces do not match. The function is UNDEFINED at x = -3, you can say the graph is continuous everywhere but where it is undefined.ĭifferentiability in Regards to Piecewise Functions Can you draw this graph without lifting your pen? No, therefore the function cannot be defined as continuous. The vertical asymptote is a point on the graph where x approaches but never reaches (from left and right side). The graph below shows the continuity of the function when a = 12, notice the vertical asymptote. In order for this piecewise function to be continuous "a" must = 12. Regular functions usually apply the same process no matter which number it is given, whereas a piecewise function will look at the number first and based on that number itself and where it is found, will decide which formula to put that number into.įor example, this is a piecewise functionį ( x ) = These intervals depend on the independent variable (x) and define the function. 5 Differentiability in Regards to Piecewise FunctionsĪ piecewise function is a function which is broken up into different pieces, each piece is defined on a certain interval.4.3 Piecewise function with an asymptote.3 Continuity in Regards to Piecewise Functions.


 0 kommentar(er)
0 kommentar(er)
